Тезисы №2 направлены к 13-му Съезду Рос. Мин. Общества (РМО).
В публикации отказано, как и посланным вместе с ними Тезисам №1 и Тезисам №3
По теме принципа Кюри см. также: Статья-1, Статья-2 , Разбор критики статьи-1
Из указанного Статья-2 – это существенно расширенный вариант данных тезисов.
Обо всех этапах моей травли в РМО (в тезисной форме) см.здесь – Уровень морали и этики в РМО
Принцип Кюри и симметрия геопроцессов
Левин Борис Самуилович. Израиль.
Кольское отделение РМО
1-й вариант. Послан в РМО 31.05.20 г. Получен отказ в публикации 30.06.20 г.
Отказы и переписку по ним см. в разделе “Этика российской науки” или конкретно здесь – Судьба моих тезисов к 13-му съезду РМО
——————————————
Принцип Кюри в приложении к геологии во всем ее объеме должен помочь при решении генетических задач восстановления геопроцессов, создавших или изменивших геологическое проявление – кристалл, горнопородное тело, тектоническую структуру и пр. Исходя из положения, что симметрия геопроцессов определяет симметрию их производных, можно решать обратную задачу – по симметрии вещественных образований восстанавливать симметрию образовавших их процессов, Конкретный инструментарий для таких работ предложен ранее (Левин, 2018)[1]. Теперь очередная задача – выявление возможных типов симметрий самих геопроцессов, и о ней – далее
——————-
Федоровские группы симметрии отражают дискретные сущности, выстроенные согласно кратной повторяемости в пространстве. Процессы, наоборот, неразрывно связаны с атрибутом времени и, так же как время, дискретности не подлежат. Отсюда, симметрия геопроцессов не может быть охарактеризована федоровскими группами, и для них надо искать другие симметрийные представления. В первом приближении процессам соответствуют предельные точечные группы симметрии (Шубников, 1956), разработанные Пьером Кюри для описания симметрии физических полей, которые тоже недискретны. Выходит, что процесс по своей структурной характеристике близок к полевым сущностям, ну а результаты процессов проявляются в вещественной среде.

1 – вращающийся конус; 2 – простой конус; 3 – вращающийся цилиндр; 4 – закрученный цилиндр; 5 – простой цилиндр; 6 – простой шар; 7 – шар с закрученными радиусами-(тензорными). Далее в тексте слово “простой” обычно опускается.
По Кюри предельных точечных групп всего семь (рис. 1). Абстрагируясь от вращающихся и закрученных осей, характеризующих особые случаи, симметрия геопроцессов в простейших ситуациях сведётся к трем типам – это три простые фигуры с осями симметрии бесконечного порядка: шар, цилиндр и конус. Шар имеет бесконечное количество осей бесконечного порядка и характеризует изотропные процессы, в которых все направления равноправны. Его иллюстрация – это покоящаяся среда. У цилиндра и конуса, в отличие от шара, только одна ось бесконечного порядка. У конуса она – направленный вектор, а у цилиндра, наоборот, она – скаляр, т.к. оба ее конца аналогичны. Конусная симметрия иллюстрируется направленным потоком, а цилиндр отражает колебательные процессы типа стоячих волн.
. На данном этапе разработки видов симметрий геопроцессов они заметно уступают в разнообразии видам симметрий вещественных тел, но по качественной характеристике последние более ограниченны. Так, процесс с симметрией цилиндра порождает тела с выделенной осью симметрии, но не всегда бесконечного порядка. Вот в кристаллах, например, эта ось ограничена только известными порядками 2, 3, 4 и 6. Т.е. процесс минералообразования имеет более высокую симметрию, чем образованные им кристаллические тела, но его симметрия необходимо включает в себя симметрию кристаллов как свою составную часть. На других уровнях геологии вещественные образования могут симметрийно совпадать с породившими их процессами (например, шаровые конкреции, образующиеся в морской среде, или же алмазоносные трубки, подчиняющиеся конусной симметрии прорыва на поверхность глубинного взрыва).
Но симметрия геопроцессов не сводится лишь к системе полевой симметрии Кюри. Это видно из ряда примеров минералогического и обще-геологического плана. Так, процесс зонального метаморфизма имеет выделенную плоскость симметрии, делящую пополам его центральную зону. По Кюри таковую имеют только цилиндры (простой и вращающийся), но их симметрии к этой ситуации не подходят, поскольку здесь мы имеем направленные изменения уровня метаморфизма в обе стороны, т.е. две векторные оси, ориентированные в противоположных направлениях. Принимая общие термины системы Кюри, здесь надо фиксировать новую группу предельной симметрии – два сопряженных конуса, зеркально отражающих друг друга (рис. 2).
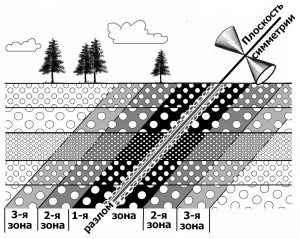
Вверху – группа симметрии этого метаморфизма.
Сходная направленность изменений (их векторность) характерна также и для контактового метаморфизма, только тут вместо центральной плоскости симметрии выступает магматический объект, и указанные векторы ориентированы по нормалям к его поверхности. При аппроксимации объемного магматического тела в виде шара получаем радиально направленные векторы градиента метаморфизма, т.е. приходим к еще одной новой группе предельной симметрии – шару с векторными радиусами, который заполнит пустующую вакансию в системе групп Кюри между двумя шарами – простым (со скалярными радиусами) и тензорным (с закрученными радиусами).
На минеральном уровне векторно-шаровая симметрия, похоже, ответственна за рост вершинных и реберных форм кристаллов. а двухконусная система симметрии, сходная с симметрией зонального метаморфизма, явно просматривается в процессе двойникования по типу «песочные часы». Однако, здесь на собственно двухконусную симметрию процесса накладываются ограничения кристаллической симметрии (по Кюри – сложение диссимметрий), и центральная плоскость симметрии может быть редуцирована до оси второго порядка. Далее, учитывая, что кристалл слагается пирамидами роста граней, можно видеть, что вообще симметрия процесса образования кристаллов соответствует пучку конусов, исходящих из точки роста кристалла.
Приведенными примерами, конечно же, не исчерпываются возможные формы симметрии геопроцессов, но и уже выведенные таковые (которые тоже не все удалось сюда вместить) вкупе с формами Кюри выстраиваются в достаточно стройную систему. Но вот развернутая статья на эту тему, при попытках ее публикации, встретила резкое сопротивление, в научном плане ничем не обоснованное. В настоящий момент вопрос о ее публикации и продолжении работы над данной концепцией остается открытым.
Литература
Левин Б.С. Приложения принципа Кюри в геологии. // Зап. РМО. 2018. №6. С.136-144
Шубников А.В. О работах Пьера Кюри в области симметрии. / Успехи физ. наук. 1956. № 59. С. 541-602.
========================================
Принцип Кюри и симметрия геопроцессов
2-й вариант. (Сравнение обеих вариантов – ниже)
Отослан в РМО 3 июля 2020 г. Отказ в публикации получен 5 июля 2020 г.
Отказы и переписку по ним см. в разделе “Этика российской науки” или конкретно здесь – Судьба моих тезисов к 13-му съезду РМО
Рисунки тут не вставлены – они такие же как и в первом варианте.
——————————————
Принцип Кюри в приложении к геологии во всем ее объеме должен помочь при решении генетических задач восстановления геопроцессов, создавших или изменивших геологическое проявление – кристалл, горнопородное тело, тектоническую структуру и пр. Исходя из положения, что симметрия геопроцессов определяет симметрию их производных, можно решать обратную задачу – по симметрии вещественных образований восстанавливать симметрию образовавших их процессов, Конкретный инструментарий для таких работ предложен ранее (Левин, 2018) Теперь очередная задача – выявление возможных типов симметрий самих геопроцессов, и о ней – далее
——————-
Федоровские группы симметрии отражают дискретные сущности, выстроенные согласно кратной повторяемости в пространстве. Процессы, наоборот, неразрывно связаны с атрибутом времени и, так же как время, дискретности не подлежат. Отсюда, симметрия геопроцессов не может быть охарактеризована федоровскими группами, и для них надо искать другие симметрийные представления. В первом приближении процессам соответствуют предельные точечные группы симметрии (Шубников, 1956), разработанные Пьером Кюри для описания симметрии физических полей, которые тоже недискретны. Выходит, что процесс по своей структурной характеристике близок к полевым сущностям, ну а результаты процессов проявляются в вещественной среде.
По Кюри предельных точечных групп всего семь (рис. 1). Абстрагируясь от вращающихся и закрученных осей, характеризующих особые случаи, симметрия геопроцессов в простейших ситуациях сведётся к трем типам – это три простые фигуры с осями симметрии бесконечного порядка: шар, цилиндр и конус. Шар имеет бесконечное количество осей бесконечного порядка и характеризует изотропные процессы, в которых все направления равноправны. Его иллюстрация – это покоящаяся среда. У цилиндра и конуса, в отличие от шара, только одна ось бесконечного порядка. У конуса она – направленный вектор, а у цилиндра, наоборот, она – скаляр, т.к. оба ее конца аналогичны. Конусная симметрия иллюстрируется направленным потоком, а цилиндр отражает колебательные процессы типа стоячих волн.
. На данном этапе разработки видов симметрий геопроцессов они заметно уступают в разнообразии видам симметрий вещественных тел, но по качественной характеристике последние более ограниченны. Так, процесс с симметрией цилиндра порождает тела с выделенной осью симметрии, но не всегда бесконечного порядка. Вот в кристаллах, например, эта ось ограничена только известными порядками – 2, 3, 4. 6. Т.е. процесс минералообразования имеет более высокую симметрию, чем образованные им кристаллические тела, но его симметрия необходимо включает в себя симметрию кристаллов как свою составную часть. На других уровнях геологии вещественные образования могут симметрийно совпадать с породившими их процессами (например, шаровые конкреции, образующиеся в морской среде, или же алмазоносные трубки, подчиняющиеся конусной симметрии прорыва на поверхность глубинного взрыва).
Но симметрия геопроцессов не сводится лишь к системе полевой симметрии Кюри. Это видно из ряда примеров минералогического и обще-геологического плана. Так, процесс зонального метаморфизма имеет выделенную плоскость симметрии, делящую пополам его центральную зону. По Кюри таковую имеют только цилиндры (простой и вращающийся), но их симметрии к этой ситуации не подходят, поскольку здесь мы имеем направленные изменения уровня метаморфизма в обе стороны, т.е. две векторные оси, ориентированные в противоположных направлениях. Принимая общие термины системы Кюри, здесь надо фиксировать новую группу предельной симметрии – два сопряженных конуса, зеркально отражающих друг друга (рис. 2).
Сходная направленность изменений (их векторность) характерна также и для контактового метаморфизма, только тут вместо центральной плоскости симметрии выступает магматический объект, и указанные векторы ориентированы по нормалям к его поверхности. При аппроксимации объемного магматического тела в виде шара получаем радиально направленные векторы градиента метаморфизма, т.е. приходим к еще одной новой группе предельной симметрии – шару с векторными радиусами, который заполнит пустующую вакансию в системе групп Кюри между двумя шарами – простым (со скалярными радиусами) и тензорным (с закрученными радиусами).
На минеральном уровне векторно-шаровая симметрия, похоже, ответственна за рост вершинных и реберных форм кристаллов. а двухконусная система симметрии, сходная с симметрией зонального метаморфизма, явно просматривается в процессе двойникования по типу «песочные часы». Однако, здесь на собственно двухконусную симметрию процесса накладываются ограничения кристаллической симметрии (по Кюри – сложение диссимметрий), и центральная плоскость симметрии может быть редуцирована до оси второго порядка. Далее, учитывая, что кристалл слагается пирамидами роста граней, можно видеть, что вообще симметрия процесса образования кристаллов соответствует пучку конусов, исходящих из точки роста кристалла.
Приведенными примерами явно не исчерпываются возможные формы симметрии геопроцессов – работы тут предстоит еще очень много.
Литература
Левин Б.С. Приложения принципа Кюри в геологии. // Зап. РМО. 2018. №6. С.136-144
Шубников А.В. О работах Пьера Кюри в области симметрии. / Успехи физ. наук. 1956. № 59. С. 541-602.
================================
Принцип Кюри и симметрия геопроцессов
Совмещенный вариант – для сравнения двух вариантов (только в сайте).
Черный цвет – общий для обоих вариантов. Красный – для 1-го. Синий – для 2-го. (т.е. при выработке 2-го варианта все красное из 1-го варианта удалено, синее – дописано).
——————————————
Принцип Кюри в приложении к геологии во всем ее объеме должен помочь при решении генетических задач восстановления геопроцессов, создавших или изменивших геологическое проявление – кристалл, горнопородное тело, тектоническую структуру и пр. Исходя из положения, что симметрия геопроцессов определяет симметрию их производных, можно решать обратную задачу – по симметрии вещественных образований восстанавливать симметрию образовавших их процессов, Конкретный инструментарий для таких работ предложен ранее (Левин, 2018)[2]. Теперь очередная задача – выявление возможных типов симметрий самих геопроцессов, и о ней – далее
——————-
Федоровские группы симметрии отражают дискретные сущности, выстроенные согласно кратной повторяемости в пространстве. Процессы, наоборот, неразрывно связаны с атрибутом времени и, так же как время, дискретности не подлежат. Отсюда, симметрия геопроцессов не может быть охарактеризована федоровскими группами, и для них надо искать другие симметрийные представления. В первом приближении процессам соответствуют предельные точечные группы симметрии (Шубников, 1956), разработанные Пьером Кюри для описания симметрии физических полей, которые тоже недискретны. Выходит, что процесс по своей структурной характеристике близок к полевым сущностям, ну а результаты процессов проявляются в вещественной среде.
По Кюри предельных точечных групп всего семь (рис. 1). Абстрагируясь от вращающихся и закрученных осей, характеризующих особые случаи, симметрия геопроцессов в простейших ситуациях сведётся к трем типам – это три простые фигуры с осями симметрии бесконечного порядка: шар, цилиндр и конус. Шар имеет бесконечное количество осей бесконечного порядка и характеризует изотропные процессы, в которых все направления равноправны. Его иллюстрация – это покоящаяся среда. У цилиндра и конуса, в отличие от шара, только одна ось бесконечного порядка. У конуса она – направленный вектор, а у цилиндра, наоборот, она – скаляр, т.к. оба ее конца аналогичны. Конусная симметрия иллюстрируется направленным потоком, а цилиндр отражает колебательные процессы типа стоячих волн.
. На данном этапе разработки видов симметрий геопроцессов они заметно уступают в разнообразии видам симметрий вещественных тел, но по качественной характеристике последние более ограниченны. Так, процесс с симметрией цилиндра порождает тела с выделенной осью симметрии, но не всегда бесконечного порядка. Вот в кристаллах, например, эта ось ограничена только известными порядками 2, 3, 4 и 6. Т.е. процесс минералообразования имеет более высокую симметрию, чем образованные им кристаллические тела, но его симметрия необходимо включает в себя симметрию кристаллов как свою составную часть. На других уровнях геологии вещественные образования могут симметрийно совпадать с породившими их процессами (например, шаровые конкреции, образующиеся в морской среде, или же алмазоносные трубки, подчиняющиеся конусной симметрии прорыва на поверхность глубинного взрыва).
Но симметрия геопроцессов не сводится лишь к системе полевой симметрии Кюри. Это видно из ряда примеров минералогического и обще-геологического плана. Так, процесс зонального метаморфизма имеет выделенную плоскость симметрии, делящую пополам его центральную зону. По Кюри таковую имеют только цилиндры (простой и вращающийся), но их симметрии к этой ситуации не подходят, поскольку здесь мы имеем направленные изменения уровня метаморфизма в обе стороны, т.е. две векторные оси, ориентированные в противоположных направлениях. Принимая общие термины системы Кюри, здесь надо фиксировать новую группу предельной симметрии – два сопряженных конуса, зеркально отражающих друг друга (рис. 2).
Сходная направленность изменений (их векторность) характерна также и для контактового метаморфизма, только тут вместо центральной плоскости симметрии выступает магматический объект, и указанные векторы ориентированы по нормалям к его поверхности. При аппроксимации объемного магматического тела в виде шара получаем радиально направленные векторы градиента метаморфизма, т.е. приходим к еще одной новой группе предельной симметрии – шару с векторными радиусами, который заполнит пустующую вакансию в системе групп Кюри между двумя шарами – простым (со скалярными радиусами) и тензорным (с закрученными радиусами).
На минеральном уровне векторно-шаровая симметрия, похоже, ответственна за рост вершинных и реберных форм кристаллов. а двухконусная система симметрии, сходная с симметрией зонального метаморфизма, явно просматривается в процессе двойникования по типу «песочные часы». Однако, здесь на собственно двухконусную симметрию процесса накладываются ограничения кристаллической симметрии (по Кюри – сложение диссимметрий), и центральная плоскость симметрии может быть редуцирована до оси второго порядка. Далее, учитывая, что кристалл слагается пирамидами роста граней, можно видеть, что вообще симметрия процесса образования кристаллов соответствует пучку конусов, исходящих из точки роста кристалла.
Приведенными примерами, конечно же, (явно) не исчерпываются возможные формы симметрии геопроцессов, но и уже выведенные таковые (которые тоже не все удалось сюда вместить) вкупе с формами Кюри выстраиваются в достаточно стройную систему. Но вот развернутая статья на эту тему, при попытках ее публикации, встретила резкое сопротивление, в научном плане ничем не обоснованное. В настоящий момент вопрос о ее публикации и продолжении работы над данной концепцией остается открытым. (работы тут предстоит еще очень много.)
Литература
Левин Б.С. Приложения принципа Кюри в геологии. // Зап. РМО. 2018. №6. С.136-144
Шубников А.В. О работах Пьера Кюри в области симметрии. / Успехи физ. наук. 1956. № 59. С. 541-602.
——————————————–
1] О критике этой концепции в ЗРМО №3 2019 см. здесь же – Левин Б.С. «Два подхода к принципу Кюри» (а здесь – Тезисы №1)